Computer Science & Engineering

https://programmers.co.kr/learn/courses/30/lessons/60061

문제 설명

이 문제는 접근 방법이 까다로웠던 문제이다. 문제의 조건은 다음과 같다.

• 기둥은 바닥 위에 있거나 보의 한쪽 끝 부분 위에 있거나, 또는 다른 기둥 위에 있어야 합니다.
• 보는 한쪽 끝 부분이 기둥 위에 있거나, 또는 양쪽 끝 부분이 다른 보와 동시에 연결되어 있어야 합니다.

문제의 입력으로 벽면의 크기 n과 기둥과 보를 설치하거나 삭제하는 작업이 순서대로 담긴 2차원 배열 build_frame이 주어진다. build_frame의 원소는 다음과 같다.

• build_frame의 원소는 [x, y, a, b]형태입니다.
  • x, y는 기둥, 보를 설치 또는 삭제할 교차점의 좌표이며, [가로 좌표, 세로 좌표] 형태입니다.
  • a는 설치 또는 삭제할 구조물의 종류를 나타내며, 0은 기둥, 1은 보를 나타냅니다.
  • b는 구조물을 설치할 지, 혹은 삭제할 지를 나타내며 0은 삭제, 1은 설치를 나타냅니다.
  • 벽면을 벗어나게 기둥, 보를 설치하는 경우는 없습니다.
  • 바닥에 보를 설치 하는 경우는 없습니다.
  • 구조물은 교차점 좌표를 기준으로 보는 오른쪽, 기둥은 위쪽 방향으로 설치 또는 삭제합니다.

위 그림에 대한 입력의 예시는 다음과 같다.

풀이

코드는 다음과 같다.

#include <string>
#include <vector>
#include <algorithm>

using namespace std;

bool graph[4][101][101]; //좌표의 상하좌우 표시

bool ans(vector<int> a, vector<int> b) { //결과 정렬 비교함수
    if(a[0] == b[0]) {
        if(a[1] == b[1]) {
            return a[2] < b[2];
        }
        else {
            return a[1] < b[1];
        }
    }
    else {
        return a[0] < b[0];
    }
}

vector<vector<int>> solution(int n, vector<vector<int>> build_frame) {
    vector<vector<int>> answer;
    for(vector<int> element : build_frame) {
        int x = element[0], y = element[1];
        int construct = element[2], install = element[3];
        
        if(install) { //설치인 경우
            if(construct == 0) { //기둥인 경우
                if(y == 0) { //바닥인 경우 그냥 설치
                    graph[0][x][y] = 1;
                    graph[1][x][y+1] = 1;
                }
                else { //바닥이 아닌 경우
                    if(graph[1][x][y] || graph[2][x][y] || graph[3][x][y]) { //보의 끝이거나 기둥 위에 올릴 수 있음
                        graph[0][x][y] = 1;
                        graph[1][x][y+1] = 1;
                    }
                }
            }
            else { //보인 경우
                if(graph[1][x][y] || graph[1][x+1][y]) { //한쪽 끝이 기둥 윗부분인 경우
                    graph[3][x][y] = 1;
                    graph[2][x+1][y] = 1;
                } 
                else if(graph[2][x][y] && graph[3][x+1][y]) { //양쪽 끝이 보인 경우
                    graph[3][x][y] = 1;
                    graph[2][x+1][y] = 1;
                }
            }
        }
        else { //제거인 경우
            if(construct == 0) { //기둥을 삭제할 경우
                bool chk = 0;
                if(graph[0][x][y+1]) { //위에 기둥이 있는 경우
                    if(!(graph[2][x][y+1] || graph[3][x][y+1]))  chk = 1; //보가 있으면 삭제 가능
                }
                if(graph[2][x][y+1]) { //왼쪽으로 보가 있는 경우
                    if(!(graph[2][x-1][y+1] && graph[3][x][y+1]) && !graph[1][x-1][y+1]) chk = 1; //양쪽에 보가 있으면 삭제 가능
                }
                if(graph[3][x][y+1]) { //오른쪽으로 보가 있는 경우
                    if(!(graph[2][x][y+1] && graph[3][x+1][y+1]) && !graph[1][x+1][y+1]) chk = 1; //양쪽에 보가 있으면 삭제 가능    
                }
                if(!chk) {
                    graph[0][x][y] = 0;
                    graph[1][x][y+1] = 0;
                }
            }
            else { //보를 삭제하는 경우
                bool chk = 0;
                if(graph[0][x][y]) { //위에 기둥이 있는 경우
                    if(!(graph[2][x][y] || graph[1][x][y])) chk = 1; //왼쪽으로 보도 없고 아래에 기둥도 없는 경우 삭제 불가
                }
                if(graph[0][x+1][y]) { //위에 기둥이 있는 경우
                    if(!(graph[3][x+1][y] || graph[1][x+1][y])) chk = 1;
                }
                if(graph[2][x][y]) { //왼쪽에 보가 있는 경우
                    if(!(graph[1][x][y] || graph[1][x-1][y])) chk = 1; //왼쪽 보가 기댈 기둥이 하나도 없는 경우 삭제 불가
                }
                if(graph[3][x+1][y]) { //오른쪽에 보가 있는 경우
                    if(!(graph[1][x+1][y] || graph[1][x+2][y])) chk = 1;
                }
                if(!chk) {
                    graph[3][x][y] = 0;
                    graph[2][x+1][y] = 0;
                }
            }
        }
    }
    for(int i = 0; i <= n; i++) {
        for(int j = 0; j <= n; j++) {
            if(graph[0][i][j]) answer.push_back({i, j, 0}); //기둥 구조물 저장
            if(graph[3][i][j]) answer.push_back({i, j, 1}); //보 구조물 저장
        }
    }
    sort(answer.begin(), answer.end(), ans); //결과 정렬
    return answer;
}

우선 마지막 조건을 보고 좌표에 시작점만을 표시한다면 문제를 풀기 굉장히 어려워진다. 따라서 3차원 배열을 이용하여 각 좌표에 상하좌우에 구조물이 있는지를 표시하였다. 그림으로 나타내면 다음과 같다.

예를 들어 (x,y)에 오른쪽과 아래로 구조물이 존재한다면 x,y 좌표의 오른쪽과 아래쪽에 해당하는 값만 1이다. 즉 다음과 같다.

graph[0][x][y] = 0; //상
graph[1][x][y] = 1; //하
graph[2][x][y] = 0; //좌
graph[3][x][y] = 1; //우

이렇게 한다면 구조물의 시작부분뿐만 아니라 끝부분도 표시할 수 있다. 1과 0의 값만 사용하기 때문에 메모리 절약을 위해 bool 타입으로 선언하였다. 설치하고 제거하는 조건은 문제에 나와있는 경우의 수를 생각해보았다.

1. 기둥을 설치하는 경우

• 만약 바닥인 경우 아무 조건 없이 설치
• 보의 끝이거나 기둥의 위인 경우 설치

2. 보를 설치하는 경우

• 한쪽 끝이 기둥 윗부분인 경우 설치
• 양쪽 끝이 보인 경우 설치

제거하는 경우는 모든 조건이 만족할 경우 제거를 할 수 있다. 따라서 제거하지 못할 조건을 체크하였다.

3. 기둥을 제거하는 경우

• 위에 기둥이 있을 경우
  • 왼쪽 오른쪽에 보가 하나도 없을 경우 제거 불가
• 왼쪽에 보가 있을 경우
  • 보의 왼쪽 오른쪽 모두 보가 존재하지 않을 경우 제거 불가
  • 보를 지탱하는 기둥이 하나도 없을 경우 제거 불가
• 오른쪽에 보가 있을 경우
  • 보의 왼쪽 오른쪽 모두 보가 존재하지 않을 경우 제거 불가
  • 보를 지탱하는 기둥이 하나도 없을 경우 제거 불가

위 조건을 모두 만족할 경우 제거 가능

4. 보를 제거하는 경우

• 바로 위에 기둥이 있는 경우
  • 왼쪽에 보가 없고 아래에 기둥도 없는 경우 제거 불가
• 제거하려는 보의 다른쪽 끝 위에 기둥이 있는 경우
  • 그 기둥을 지탱하는 보나 기둥이 없는 경우 제거 불가
• 왼쪽에 보가 있는 경우(한쪽이 연결된 보가 제거되므로 기둥만 생각하면 됨)
  • 보가 지탱할 기둥이 하나도 없는 경우 제거 불가
• 오른쪽에 보가 있는 경우
  • 보가 지탱할 기둥이 하나도 없는 경우 제거 불가

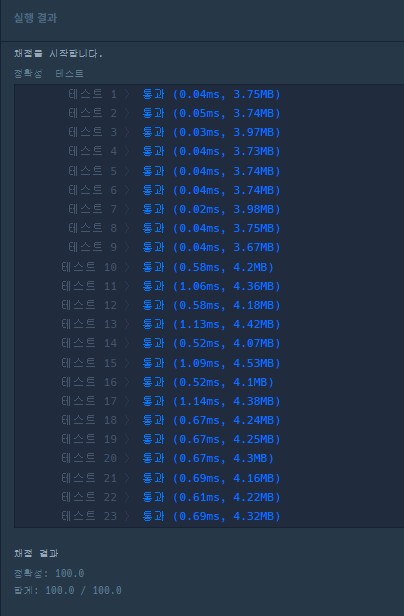
위의 규칙에 따라 기둥을 하나씩 설치하고 제거한 다음 구조물이 그래프에 완성된다. 구조물의 결과를 리턴해야하므로 각 좌표를 하나씩 순회하며 기둥은 위로, 보는 오른쪽으로 설치하므로 graph의 1차원 인덱스가 0이나 3일 경우 값이 참일 때 정답 벡터에 좌표와 기둥인지 보인지를 push_back해준다. 모두 넣은 다음 answer를 조건에 따라 정렬하여 리턴하면 된다. 위 코드를 실행할 경우 다음과 같이 모두 통과하는 것을 볼 수 있다.

이번에는 여러가지 알고리즘을 사용할 때 꼭 필요한 queue를 구현해보았다. STL의 queue에서 제공하는 priority_queue는 따로 minheap, maxheap으로 따로 구현하도록 하겠다. 우선 구현한 코드는 아래 링크에서 확인할 수 있다.

https://github.com/Seo-sang/Cpp-_Standard_Template_Library/blob/master/myqueue.cpp

queue란?

    queue(큐)는 stack과 같은 기본적인 자료구조로 가장 마지막으로 들어간 원소가 가장 먼저 나오는 LIFO(Last In First Out)인 stack과 다르게 가장 먼저 들어간 원소가 가장 먼저 나오는 FIFO(First In First Out)이다. queue를 그림으로 표현하면 다음과 같다.

그림과 같이 한쪽은 나올 수 만 있는 출구가 있고 다른 한 쪽은 들어갈 수만 있는 입구가 있다. queue안에서 순서는 바뀌지 않는다. 따라서 들어간 순서와 나오는 순서가 똑같다. 큐에 원소를 넣는 것을 'push'라고 하고 원소를 빼는 것을 'pop'이라고 한다. 위 그림은 1부터 6까지 push한 상태에서 1번 pop을 하고 7을 push하려고 하는 상태이다.

구현

     큐의 구현은 여러가지로 할 수 있다. 배열로 구현하는 것은 간단하지만  pop을 여러번 하는 경우 배열의 크기는 일정하기 때문에 배열의 앞 부분은 비어있는 상태가 될 수 있다. 또 배열의 크기보다 push를 많이 하는 경우 새로 할당해줘야하는 등의 오버헤드가 있기 때문에 그러한 번거로움을 줄일 수 있는 연결리스트로 구현하였다. 연결 리스트를 이용하여 구현하였기 때문에 이전 글 만들었던 list와 비슷한 부분이 많았다. 우선 각 노드를 나타내는 구조체는 아래와 같다.

struct node {
    T data; //값이 들어가는 변수
    node* next; //다음 노드를 가리키는 포인터

    node(T input) { //생성자
        data = input; //input을 준 경우 input으로 data를 설정
        next = NULL; //다음 노드는 NULL포인터로 설정
    }
    
    node() { //생성자
        data = 0; //input이 없는 경우 0으로 초기화
        next = NULL; //다음 노드는 NULL포인터로 설정
    }
};

STL queue에서 제공하는 대부분의 함수를 구현하였다. iterator가 없기 때문에 굉장히 간단했다. 구현한 메소드로는 empty, size, front, back, push, pop, swap이 있다.

실행 결과

1. push, pop 실행 결과

int main() {
    myqueue<int> q1;
    for(int i = 1; i <= 10; i++) //q1에 1부터 10까지 넣음
        q1.push(i);
    
    while(!q1.empty()) { //q1 출력
        cout << q1.front() << ' ';
        q1.pop();
    }
}

2. front, back 실행 결과

int main() {
    myqueue<int> q1;
    for(int i = 1; i <= 10; i++) //q1에 1부터 10까지 넣음
        q1.push(i);
    
    cout << "front : " << q1.front() << "\nback : " << q1.back() << endl; //front, back 출력

    while(!q1.empty()) { //q1 출력
        cout << q1.front() << ' ';
        q1.pop();
    }
}

3. swap 실행 결과

int main() {
    myqueue<int> q1, q2;
    for(int i = 1; i <= 10; i++) //q1에 1부터 10까지 넣음
        q1.push(i);
    
    for(int i = 101; i <= 110; i++) //q2에 101부터 110까지 넣음
        q2.push(i);

    q1.swap(q2); //q1과 q2 swap

    while(!q1.empty()) { //q1 출력
        cout << q1.front() << ' ';
        q1.pop();
    }
    
    cout << endl;

    while(!q2.empty()) { //q2 출력
        cout << q2.front() << ' ';
        q2.pop();
    }
    
}

이렇게 간단한 자료구조 queue를 구현해보았다. 우선순위 큐는 따로 minheap과 maxheap으로 구현하도록 하겠다.

https://programmers.co.kr/learn/courses/30/lessons/72414

이 문제는 큐를 브루트 포스로 풀었을 경우 O(n^2)의 시간 복잡도를 가지며 시간초과가 발생한다. 처음 이 풀이를 사용하지 않았을 때 테스트케이스 마지막 3개는 시간초과로 통과하지 못하였다. 그렇기 때문에 O(n)의 시간복잡도를 가지는 풀이를 사용해야했다. 문제를 보면 시간은 ms단위가 없기 때문에 정수형으로 시간을 바꾸었을 때 생각보다 큰 숫자가 나오지 않는다. 우선 카카오에서 자주 출제되는 시간을 문자열로 주어지는 문제는 가장 작은 단위로 통일하여 시간을 계산해주는 것이 좋다. 나는 toint()라는 함수를 만들어 string을 초 단위의 정수형으로 변환하는 함수를 만들어 사용하였다. 코드는 아래와 같다.

#include <string>
#include <vector>
#include <queue>
#include <map>
#include <algorithm>

using namespace std;

int arr[360000];

int toint(string str) { //문자열 시간을 정수형으로 변환
    int h = stoi(str.substr(0, 2));
    int m = stoi(str.substr(3, 2));
    int s = stoi(str.substr(6, 2));
    int ret = s;
    ret += (m * 60);
    ret += (h * 3600);
    return ret;
}

string tostr(int time) { //정수형 시간을 문자열로 변환
    string ret = "";
    int h = time / 3600;
    time %= 3600;
    int m = time / 60;
    time %= 60;
    int s = time;
    if(h < 10) //1자리일 경우 0 추가
        ret += '0';
    ret += to_string(h);
    ret += ":";
    if(m < 10) //1자리일 경우 0 추가
        ret += '0';
    ret += to_string(m);
    ret += ":";
    if(s < 10) //1자리일 경우 0 추가
        ret += '0';
    ret += to_string(s);
    
    return ret;
}

string solution(string play_time, string adv_time, vector<string> logs) {
    string answer = "";
    int adv = toint(adv_time); //광고 시간 정수형으로 변환
    int play = toint(play_time); //재생 시간 정수형으로 변환
    long long mnum = 0; //최대값 저장
    long long sum = 0; //현재 누적시간
    int idx = 0; //최대값의 시작시간 저장
    for(string str : logs) {
        int s = toint(str.substr(0, 8)); //시작시간
        int e = toint(str.substr(9)); //종료시간
        for(int i = s; i < e; i++) arr[i]++; //log들이 재생한 구간 표시
    }
    
    for(int i = 0; i < adv; i++) { //00:00:00부터 광고 시간만큼 재생한 수 계산
        sum += arr[i];
    }
    
    mnum = sum;
    
    for(int i = adv; i < play; i++) { //1초씩 늘려가며 
        sum -= arr[i - adv]; //1초 전 시청인원 빼기
        sum += arr[i]; //다음 1초 시청인원 추가
        if(mnum < sum) { //최대인 경우
            idx = i - adv + 1; //최대값에서의 시작 시간 저장
            mnum = sum; //최대값 갱신
        }
    }
    
    answer = tostr(idx); //최대값에서의 시작시간을 string으로 변환
    
    return answer;
}

이 문제는 광고 재생 시간이 일정하게 유지된다. 따라서 00:00:00초부터 종료시간까지 광고 시간이 슬라이딩하며 그 시간에 시청한 사람들의 수를 계산할 수 있다. 예를 들면 광고 재생 시간이 10초인 경우

 0초~9초 -> 1초~10초 -> 2초~11초 -> ...

이런 식으로 처음 시작 시간에 시청한 인원을 빼고 그 다음 초에 시청한 인원을 더하며 슬라이딩 방식을 사용한다면 O(n)만에 모든 시간에서 최대 인원이 시청한 시간을 알 수 있다. 하나를 빼고 하나를 더할 때마다 최대값인지를 확인하며 최대값인 경우 그때의 광고 시작 시간을 저장한다. 시작 시간은 정수형이기 때문에 마지막에 그 최대값을 문자열로 변환하여 리턴해주면 된다.

카카오에서 이런 문자열을 다루는 문제가 자주 나오기 때문에 문자열을 다루는 라이브러리 함수 특히 substr, stoi 등을 익혀놓는 것이 문제를 풀 때 상당히 도움이 된다.

이번에는 C++에서 제공하는 Standart Template Library의 <list>를 구현해보았다. list는 linked list(연결리스트)를 구현한 것이며 특징으로는 iterator를 제공하고 양방향 연결리스트라는 것이다. cplusplus.com에 검색하면 나오는 list의 모든 메소드들을 구현하지는 못하였고 많이 쓰이는 메소드 몇 가지만 구현하였다. 소스코드는 아래의 링크에서 확인할 수 있다.

https://github.com/Seo-sang/Cpp-_Standard_Template_Library/blob/master/mylist.cpp

연결리스트는 컴퓨터 전공생이면 1학년부터 C언어에서 포인터를 배우며 누구나 구현해보았을 것이다. 양방향 연결리스트도 이전노드와 연결해주는 것만 포함하면 전혀 다를 것이 없이 쉽게 구현할 수 있다. 따라서 이 구현에서 새로웠던 점은 iterator구현이다. list의 iterator 구현을 위한 특징이 하나 있다. 아래는 mylist의 멤버 변수이다.

멤버변수

public:
    node* head; //시작 노드
    node* tail; //마지막 노드
    node* fin; //end 노드
    int num; //노드 수

head와 tail은 첫 번째 노드와 마지막 노드를 가리킨다. iterator에서는 end가 존재한다. end는 연결리스트의 노드가 아니며 마지막만을 나타내는 기능을 제공한다. 즉 데이터가 들어있지 않다. 따라서 list에 아무것도 들어있지 않았어도 end를 가리키는 fin노드는 존재하여 유지시켰다.

iterator

class myiterator {
        node* current;
    public:
        myiterator(node* node = 0) : current(node) {};

        myiterator& operator++() {
            current = current->next;
            return *this;
        }
        
        myiterator& operator--() {
            current = current->prev;
            return *this;
        }

        node* operator&() {
            return current;
        }

        T& operator*() {
            return current->data;
        }

        bool operator !=(const myiterator& cmp) {
            return (current != cmp.current);
        }

        bool operator ==(const myiterator& cmp) {
            return (current == cmp.current);
        }
    };

iterator는 vector를 구현했을 때와 비슷하다. 연산자는 ++, --, *, !=, ==를 구현하였고 &연산자는 iterator로부터 포인터 값을 얻기 위해 내가 따로 만들었다. 물론 사용자도 사용할 수 있다. ++와 --는 각각 다음 노드, 이전 노드로 이동하는 연산자이다. iterator를 이용한 연결리스트를 순회할 때 굉장히 유용하게 사용할 수 있다. * 연산자는 현재 노드의 데이터 값을 얻어오는 연산자이다. ==와 !=는 각각 두 iterator변수가 같은 노드를 가리키는지 다른 노드를 가리키는지를 판단하는 연산자이다.

methods

구현한 메소드를 나열해보면

size, empty, front, back, push_back, pop_back, push_front, pop_front, insert, erase, begin, end로 총 12가지이다. 메소드는 모두 cplusplus.com에서 list를 검색했을 때 나오는 메소드와 똑같이 동작한다. 아래에서 실제 실행 결과로 보여주겠다. 코드가 길어 소스코드는 위의 링크에서 확인할 수 있다.

실행결과

이 코드는 아래와 같이 동작한다.

    1. 1부터 10까지 push_back을 한 다음 출력

    2. 3번 pop_back()을 한 다음 출력

    3. 100부터 3번 push_front한 다음 출력

    4. 6번 pop_front한 다음 출력

실행 결과는 다음과 같이 올바르게 나오는 것을 알 수 있다. iterator를 이용하여 모든 노드의 데이터를 출력하는 것도 올바르게 동작하는 것을 확인할 수 있다.

이번에는 insert와 erase를 사용해보겠다.

이 코드는 다음과 같이 동작한다.

    1. 1부터 10까지 push_back하고 출력

    2. begin부터 2번 다음 노드로 이동 후 100 insert 하고 출력

    3. 그 다음 3번 다음 노드로 이동 후 erase하고 출력

결과는 다음과 같다.

실행 결과 begin부터 2번 이동한 3번 위치에서 insert를 수행할 경우 3번 위치에 100을 삽입하고 3부터는 뒤로 밀리는 것을 알 수 있다. 그 다음 3번 위치부터 3번 이동한 6번 노드에서 erase연산을 수행하여 6번 노드가 사라진 최종 결과가 정확히 나왔음을 확인할 수 있다.

이렇게 C++ STL의 list의 일부를 직접 구현해보았다. 연결리스트를 직접 구현할 경우 예상치 못한 널포인터로 segmentation fault가 발생하는 것을 자주 접할 수 있다. 글쓴이 역시 list를 구현하며 몇 번의 segmentation fault를 보았다. 하지만 포인터 관리만 잘해주면 오류를 쉽게 찾고 고칠 수 있기 때문에 이렇게 직접 구현해보며 실수를 깨달을 수 있었다.

https://programmers.co.kr/learn/courses/30/lessons/64062

문제의 카테고리가 이분탐색인 것을 알지 못하고 문제를 본다면 이분탐색을 이용하여 문제를 풀어야 한다는 것을 알아차리기가 쉽지 않다. 며칠 전에 이분탐색 여러 문제를 풀어보았기 때문에 문제를 읽고 이분탐색을 사용하면 잘 될 것이라고 생각하여 문제 접근 방향을 그렇게 정하였다. 코드는 굉장히 짧다. 아래와 같다.

소스코드

#include <string>
#include <vector>
#include <algorithm>

using namespace std;

int solution(vector<int> stones, int k) {
    int answer = 0;
    int left = 0, right = *max_element(stones.begin(), stones.end()) + 1; //초기값 설정
    for(int i = 0; i < 30; i++) { //최대 200000000이므로 log2 200000000은 30보다 충분히 작으므로 가능하다.
        int mid = (left + right) / 2; //중간 값을 설정한다. mid명이 건넌다고 생각한다.
        int maxcnt = 0; //가장 많이 건너뛴 수를 저장
        int cnt = 1; //건너뛴 횟수를 그때그때 저장
        for(int i = 0; i < stones.size(); i++) { //징검다리를 하나씩 보며
            if(stones[i] < mid) cnt++; //mid번째 사람이 건널 경우 mid보다 작은 값이 있는 돌은 mid-1명만 건널 수 있으므로 건너뛰게 된다. 따라서 숫자를 센다.
            else { //만약 mid보다 크거나 같은 경우 mid번째 사람도 돌을 밟을 수 있으므로 한번에 건너뛰는 돌의 수는 1로 다시 초기화하고 현재 돌까지 한번에 건너뛴 돌의 수를 계산
                maxcnt = max(maxcnt, cnt); //한번에 건너뛴 돌의 최대값 갱신
                cnt = 1;
            }
        }
        maxcnt = max(maxcnt, cnt); //마지막 돌까지 건널때 cnt값이 갱신되지 않을 수 있으므로 한 번 더 체크
        if(maxcnt <= k) left = mid; //최대 k개 건너 뛸 수 있으므로 가장 많이 건너뛴 수가 k보다 작거나 같은 경우 더 많은 인원이 건널 수 있다고 판단
        else right = mid; //그렇지 않으면 더 적은 사람이 건너 뛸 수 있다고 판단
    }
    answer = left; //등호가 left에 있으므로 left값이 최종 결과
    return answer;
}

이분탐색을 할 때 결과값이 left냐 right냐를 아는 것은 꽤 어렵다. 이 문제는 최대값을 구해야하는 문제이므로 등호를 포함하는 값이 정답이 될 것이다. 글쓴이는 거의 left에 등호를 붙인다.

풀이에서 중요한 부분

    1. left는 초기값으로 0, right는 최대값보다 1 큰 값으로 설정하였다. 1을 더한 이유는 만약 left = 5, right = 6일 경우 mid값으로 갱신했을 경우 mid는 항상 5이므로 left는 6이 될 수 없다. 만약 정답이 6일 경우 오답이 나올 수 있다. 따라서 left는 최소값보다 작은 값, right는 최대값보다 큰 값으로 설정하는 것이 좋다.

    2. for문을 30번 돌았다. stone배열의 원소의 최대값은 200000000(2억)이다. 따라서 2억을 커버할 수 있는 30으로 설정하였다. log2의 200000000은 30보다 훨씬 작은 수이다. 2^30은 대락 10의 9제곱이기 때문이다. 2억을 넘을 수 있는 log값으로 더 작은 수로 설정하여도 충분히 돌아간다.

    3. left가 정답인 이유는 파라매트릭 문제를 여러번 풀어봐야한다. 이 문제에서는 건너뛴 바위의 수가 k보다 작거나 같은 조건에서 가장 큰 값이어야한다. 이때 for문의 가장 마지막에 if(maxcnt <= k) left = mid;라는 코드가 있다. 이 코드가 바로 이전 말과 같은 말이다. 건너뛴 바위의 수가 k보다 작거나 같을 때 left를 mid로 설정하라는 말이다. 더 큰 값이 있을 수 있기 때문이다. 만약 이 조건을 만족하지 않을 경우 right = mid 코드가 실행될 것이다. 따라서 left는 정답이 될 수 있는 조건을 만족하지 않은 상태에서 최대값으로 갱신되기 때문에 left가 최종 정답이 되는 것이다.

https://programmers.co.kr/learn/courses/30/lessons/72413

이 문제는 딱 보자마자 플로이드-와샬 알고리즘으로 쉽게 풀 수 있는 문제임을 직감했다. 모든 정점에서 다른 모든 정점으로의 최단 경로를 구한 다음 시작정점으로부터 한 지점을 거쳐서 각각 A, B의 집을 가는 경로의 최솟값을 구하면 된다. 코드는 다음과 같다.

#include <string>
#include <vector>
#include <algorithm>
#include <iostream>

using namespace std;

const int MN = 201;
const int INF = 1e9; //무한대

int floyd[MN][MN]; //최단 경로를 저장할 배열

int solution(int n, int s, int a, int b, vector<vector<int>> fares) {
    int answer = INF;
    fill(&floyd[0][0], &floyd[n][n+1], INF); //최단 경로 무한대로 초기화
    for(int i = 1; i <= n; i++)
        floyd[i][i] = 0; //자기 자신은 0으로 초기화
    
    for(vector<int> e : fares) { //u->v와 v->u 모두 가능하므로 양방향으로 초기화
        floyd[e[0]][e[1]] = e[2];
        floyd[e[1]][e[0]] = e[2];
    }
    for(int k = 1; k <= n; k++) { //플로이드-와샬 알고리즘 수행 k정점을 통해 갔을 경우를 각각 계산
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= n; j++) {
                floyd[i][j] = min(floyd[i][j], floyd[i][k] + floyd[k][j]);
            }
        }
    }
    
    for(int k = 1; k <= n; k++) { //1번 정점부터 n번 정점까지 출발점부터 k를 지나 a, b로 각각 가는 합 계산
        int tmp = floyd[s][k] + floyd[k][a] + floyd[k][b];
        if(tmp < 0) continue; //오버플로우 방지
        answer = min(answer, tmp); //최솟값 갱신
    }
    
    return answer;
}

    초기화를 1e9인 10억으로 했기 때문에 만약 s->k, k->a, k->b 경로가 모두 없는 경우 30억으로 약 21억인 정수형 범위를 넘어가게 된다. 그렇기 때문에 오버플로우 방지로 계산한 결과 값이 0보다 큰 경우에만 최소값을 갱신해야한다. 그렇지 않으면 엄청나게 작은 수가 최소값으로 갱신될 것이다.

    플로이드-와샬 알고리즘을 수행하는 부분은 가운데에 있는 3중 반복문이다. k정점을 지나는 경우를 계속 최단 경로로 갱신하여 모든 정점에서 다른 모든 정점으로의 최단 경로를 구할 수 있다. 한 정점에서 다른 모든 정점으로의 최단 경로를 구하는 다익스트라나 벨만-포드 알고리즘은 O(n^2)의 알고리즘이 가능하지만 모든 정점에서의 최단 경로를 모두 구하는 플로이드-와샬 알고리즘은 O(n^3)의 알고리즘이 최선이다. 문제의 조건에 따라 다익스트라를 사용할지 플로이드-와샬 알고리즘을 사용할지 잘 판단해야한다.

https://programmers.co.kr/learn/courses/30/lessons/17678

이 문제는 조건을 차근차근 맞춰나가면 충분히 풀 수 있는 문제이다. 핵심은 버스의 수, 버스 1대당 탈 수 있는 인원의 수를 생각해야한다는 점이다. 시간관련 문제를 풀 때 모든 시간을 가장 작은 단위로 통일하는 것이 굉장히 편하다. 이 문제에서는 가장 작은 단위가 분이므로 모든 시간을 몇분인지 계산하면 쉽게 구할 수 있다. 특히 소수점이 나오는 시간문제는 부동 소수점으로 계산할 경우 계산 과정에서 원하는 값이 나오지 않을 수 있으므로 integer형으로 계산하는 것이 가장 좋다. 코드는 다음과 같다.

#include <string>
#include <vector>
#include <algorithm>

using namespace std;

bool cmp(string a, string b) { //내림차순 정렬
    return a > b;
}

int part(string a) { //string을 시간으로 변경
    pair<int,int> hm;
    hm.first = stoi(a.substr(0, 2)); //hour 분리
    hm.second = stoi(a.substr(3, 2)); //minute 분리
    int ret = hm.first * 60; //분으로 합치기
    ret += hm.second;
    return ret;
}

string timetostring(int time) { //시간을 string으로 변경
    string ret = "";
    int h = time / 60; //hour 분리
    int m = time % 60; //minute 분리
    if(h < 10) //1자리 수인 경우 앞에 '0' 붙이기
        ret += '0';
    ret += to_string(h);
    ret += ':';
    if(m < 10) //1자리 수인 경우 앞에 '0' 붙이기
        ret += '0';
    ret += to_string(m);
    return ret;
}

string solution(int n, int t, int m, vector<string> timetable) {
    string answer = "";
    sort(timetable.begin(), timetable.end(), cmp); //내림차순으로 정렬
    int now = 540; //9시 정각
    int end = now + (t * (n-1)); //버스 마지막 시간
    int cnt = 0; //마지막 버스 탑승자 카운트
    for(int i = 0; i < n; i++) { //n개의 버스
        if(i == n - 1) { //마지막 버스일 경우
            if(cnt == m - 1) break; //1자리 남은 경우 break
        }
        if(timetable.empty()) break; //모두 탄 경우 break
        for(int j = 0; j < m; j++) { //m개의 탑승자 수 만큼
            if(timetable.empty()) break; //모두 탄 경우 break
            int hm = part(timetable.back()); //가장 빨리온 사람 시간으로 변경
            if(hm <= now) { //현재 버스를 탈 수 있는 경우
                timetable.pop_back(); //버스에 탑승
                if(i == n - 1) { //마지막 버스인 경우
                    cnt++; //탑승자 수 증가
                    if(cnt == m-1) break; //마지막 버스 1자리 남은 경우 break
                }
            }
            else { //가장 빨리온사람도 현재 버스를 탈 수 없는 경우 break
                break;
            }
        }
        now += t; //다음 버스
    }
    if(timetable.empty()) { //모두 버스에 타고도 자리가 남은 경우
        answer = timetostring(end); //마지막 버스 탑승
    }
    else {
        int back = part(timetable.back()); //남은 탑승자 중에 가장 빠른 사람
        if(back > end) { //마지막 버스보다 뒤에 오는 경우
            answer = timetostring(end); //콘은 마지막 버스 탑승
        }
        else { //남은 탐승자 중에 가장 빠른 사람이 버스를 탈 수 있는 경우
            back--; //콘은 1분 일찍 도착해서 버스 탑승
            answer = timetostring(back);
        }
    }
    return answer;
}

이 문제에서 중요한 것은 마지막 버스이다. 마지막 버스에 자리가 있는지 없는지를 판단하는 것이다. 각 버스에 최대 m명을 태울 수 있으므로 버스가 오는 시간까지 기다리고 있는 사람은 버스에 태워 보낸다. m명이 모두 차지 않더라도 정류장에 도착한 사람이 없는 경우 버스는 출발한다. 마지막 버스가 도착했을 때 m-1명까지만 버스에 태운다. 마지막 1자리는 콘이 타야하기 때문이다. 그리고 프로그램 마지막에 판단한다. 이때 경우의 수가 3가지가 있다.

    1. 만약 정류장에 기다리는 사람이 없는 경우 콘은 마지막 버스가 출발하는 시간에 도착하면 된다.

    2. 만약 정류장에 사람이 기다리고 있지만 그 사람은 마지막 버스가 출발하는 시간보다 늦게 오는 경우 1번과 마찬가지로 마지막 버스의 시간과 같으면 된다.

    3. 마지막으로 남은 탑승자가 마지막 버스가 출발하는 시간보다 먼저 와서 기다리는 경우 그 사람보다 1분 먼저 도착하면 된다. 그렇다면 가장 높은 우선순위이기 때문에 마지막 1자리를 탈 수 있다.

이렇게 버스는 n개, 버스 하나 당 m명 탑승 가능이라는 조건을 하나하나 맞춰 나가고 마지막 1자리를 콘이 탈 수 있는 조건으로 위의 3가지 경우만 생각할 경우 문제를 쉽게 풀 수 있다. 이 문제의 핵심은 string으로 주어진 시간을 integer형으로 바꾸어 계산을 편하게 한 점과 조건을 하나하나 맞춰 경우의 수를 나누어 풀은 부분이라고 생각한다.

https://programmers.co.kr/learn/courses/30/lessons/77486

이 문제는 읽어보면 아주 간단한 문제이다. 문제를 읽고 DFS방식으로 풀면 금방 풀릴 것이라는 생각이 바로 들 것이다. 다단계에서 판매하는 칫솔의 수익의 10퍼센트를 자신을 추천한 사람에게 줄 때 사람들의 수익을 구하는 문제이다. 코드는 다음과 같다.

#include <string>
#include <vector>
#include <map>
using namespace std;

map<string,string> graph; //누구에게 추천받았는지를 저장
map<string, int> cost; //각 사람이 번 돈을 저장할 map

void dfs(string now, int amount) { //현재 사람이 번 돈
    string ref = graph[now]; //추천인이 누군지 찾음
    int nxt = amount / 10; //10퍼센트 떼서
    if(ref == "-") { //center를 만날 경우
        cost[now] += (amount - nxt); //자기 자신은 10퍼센트를 떼고 얻음
        return;
    }
    else { //추천인이 center가 아닌 경우
        int nxt = amount / 10; //10퍼센트를 떼서
        cost[now] += (amount - nxt);  //자기 자신은 나머지를 갖고
        if(nxt == 0) return; //만약 10퍼센트가 1원도 안나올 경우 dfs 멈춤
        dfs(ref, nxt); //추천인에게 줄 돈이 남은 경우 추천인의 추천인 계속 탐색
    }
}

vector<int> solution(vector<string> enroll, vector<string> referral, vector<string> seller, vector<int> amount) {
    vector<int> answer;
    for(int i = 0; i < enroll.size(); i++) { //모든 사람에 대하여
        graph[enroll[i]] = referral[i]; //자신을 추천한 사람 map으로 연결
    }
    
    for(int i = 0; i < seller.size(); i++) { //판매한 사람 모두 dfs로 추천인에게 10퍼센트씩 부여
        dfs(seller[i], amount[i] * 100); //칫솔 1개에 100원이므로 판매 수에 100을 곱한다
    }
    
    for(int i = 0; i < enroll.size(); i++) {
        if(cost.find(enroll[i]) == cost.end()) //만약 수익이 없는 사람을 발견할 경우
            answer.push_back(0); //0원 push_back
        else
            answer.push_back(cost[enroll[i]]); //map에 저장한 수익 push_back
    }

    return answer;
}

    DFS를 이용하여 자신의 추천인에게 10퍼센트를 계속 떼어 주는 것이다. 만약 현재 돈이 10원 미만이어서 10퍼센트를 떼었을 경우 1원도 나오지 않을 경우 DFS를 빠져나오게 된다. 저 조건을 뺄 경우 몇몇 테스트 케이스에서 시간초과가 발생한다. 불필요한 탐색을 거르는 장치인 것이다.

    그래프와 각 사람이 번 돈들을 map으로 표현하는 것이 핵심이었다. 다른 표현 방법으로 각 사람을 인덱스 번호로 표현하여 각각 사람의 인덱스를 가지고 있고 찾아봐야할텐데 map을 이용하여 그러한 시간을 줄이고 더 편하게 이름으로 사람을 찾을 수 있었다.

    문제의 설명이 길어 긴장했지만 읽어보니 굉장히 단순하게 풀 수 있는 방법이었다. DFS 재귀 방식 말고도 while문을 이용하여 더 빠른 시간에 풀 수 있는 방법도 있으니 그 방법도 생각해보면 좋을 것 같다.