https://www.acmicpc.net/problem/2565
2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net

풀이
이 문제는 LIS를 이용해 풀면 쉽게 풀 수 있는 문제이다. 우선 왼쪽 전봇대에 연결된 위치 순서의 오름차순으로 정렬한다. 하나의 위치에 하나의 전깃줄만 연결되어 있으므로 중복되는 번호는 존재하지 않는다. 그렇다면 이제부터 오른쪽 전봇대에 연결된 위치만 생각하면 된다. 오른쪽 전봇대에 연결된 위치의 번호의 LIS의 최대 길이가 전깃줄을 최소로 제거하는 방법이다. 그림으로 보면 아래와 같다.
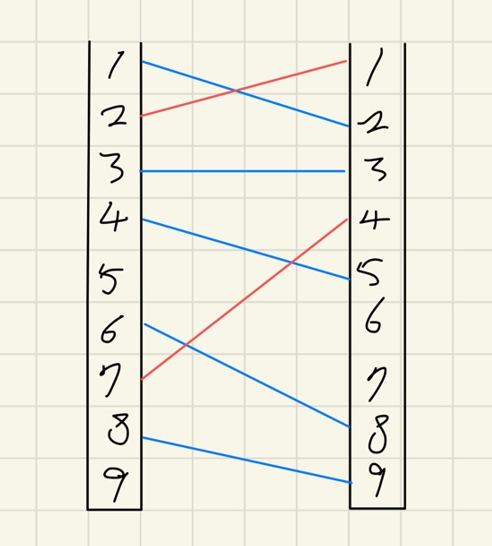
파란색 선이 꼬이지 않고 최대로 연결한 방법이고 빨간 선이 삭제해야하는 전깃줄이다. 번호를 보면 왼쪽 번호가 증가함에 따라 오른쪽 번호도 당연히 증가하는 것을 알 수 있다. 만약 오른쪽 번호가 증가하다 감소하면 전깃줄이 꼬였다는 이야기이다. 따라서 이 문제는 왼쪽 전봇대의 번호 순으로 정렬한 다음 오른쪽 전깃줄 번호의 가장 긴 증가하는 부분 수열의 길이를 구하는 문제이다. 코드는 다음과 같다.
소스 코드
#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
vector<pair<int,int>> arr;
vector<int> dp;
bool cmp(pair<int,int> a, pair<int,int> b) { //왼쪽 전봇대 번호 정렬
return a.first < b.first;
}
int main() {
int N; cin >> N;
for(int i = 0; i < N; i++) {
int a, b; cin >> a >> b;
arr.push_back({a,b});
}
sort(arr.begin(), arr.end(), cmp); //정렬
dp.push_back(-1); //초기값 설정
for(int i = 0; i < N; i++) { //LIS 최대 길이 구하기
if(dp.back() < arr[i].second) { //가장 큰 원소보다 큰 경우 뒤에 push
dp.push_back(arr[i].second);
}
else { //그렇지 않은 경우 이진탐색을 이용하여 알맞은 위치에 교체
auto it = lower_bound(dp.begin(), dp.end(), arr[i].second);
*it = arr[i].second;
}
}
cout << N - (dp.size()-1); //총 개수 N에서 최대 LIS 길이를 뺀 수만큼 전깃줄 제거해야함
}
채점 결과

'알고리즘 > 백준' 카테고리의 다른 글
| [C++] 백준 13458번 시험 감독 풀이 (0) | 2021.08.21 |
|---|---|
| [C++] 백준 3190번 뱀 풀이 (0) | 2021.08.21 |
| [C++] 백준 12015번 가장 긴 증가하는 부분 수열 2 풀이 (0) | 2021.08.14 |
| [C++] 백준 11053번 가장 긴 증가하는 부분 수열 풀이 (0) | 2021.08.13 |
| [C++] 백준 2110번 공유기 설치 풀이 (0) | 2021.08.08 |